여름방학동안 친 코드포스 개강하고 업솔빙하기
#1 도입
방학동안 약10번 가량의 Contest를 참가했는데 제대로 upsolving을 한적이 없다는 사실을 학교가는 길에 깨달았다. 소잃고 외양간을 고쳐보자
codeforces Round 969 (Div. 2)
D. Iris and Game on the Tree
- 어떤 문자열 110101111000 이 있을때, 이전과 같은 숫자는 의미가 없기에 101010 으로 생각한다
- 101010에서 101과 같이 1에서0을갔다가 다시1로오면 상쇄되므로 101이나 010 1과 0으로 봐도 된다.
- 문자열을 치환하다보면 맨앞과 맨뒤가 다르면 합산 1or-1 , 맨앞맨뒤가 같으면 합산0 임을 알 수 있다.
- 즉 루트와 리프에 어떤값이 들어가는지가 score를 결정한다.
배운점
-
함수 인자로 벡터나 배열을 전달할 때에는 참조자를 붙이는 것을 까먹지 말자.
-
루트와 리프는 트리에서 자신을 제외한 1가지의 노드에게만 연결된다. 따라서
if(adj[i].size()==1)과 같이 간단한 코드로 리프인지를 판단할 수 있다.
-
랭커들의 코드를 보고 게임 이론을 구현하는 스타일에 대해 공부해보았다
while(root==2 || cnt[2]>0) { if(it==0) {//첫번째 플레이어 if(root==2) { if(cnt[0]==cnt[1] && skip%2==1) { //player1 차례에 skip이 홀수개이고 리프의 0과1 개수같다면 상대가 선택할 //때까지 skip을 고르는게 이득이므로 skip을 선택한다 //짝수일때는 서로 의미가 없으므로 바로0으로 만들어도 상관이 없다. skip=0; } else { root = (cnt[0]>cnt[1] ? 1 : 0); } } else { //root와 반대되는 숫자를 리프에 넣어준다 cnt[2] -= 1; cnt[root ^ 1]++; } } else { if(root ==2) { root = (cnt[0]>cnt[1] ? 1:0); } else { //player2는 root와 같은 숫자를 리프에 넣는다 cnt[2]--; cnt[root]++; } } //다음순서로 바꾸어준다 it ^=1; }- 삼항연산자로 코드를 간단히 하는 습관을 들이자
- a^1 은 짝수면 1을 더하고 홀수면 1을뺀다 이를 이용해 0과1을 번갈아 이동할 수 있다.
E. Iris and the Tree
-
트리가 dfs order를 가지기 때문에, 연속한 노드 사이거리 합은 모든 간선을 오직 2번씩 더한 값이다. (내려갈때 올라갈때)
- $i$→ $p_i$ 가중치를 사용하는 경우는 $(i-1)$→ $i$ 과 $i$ 의 subtree 에서 가장 큰값에서 다음으로 이동하는 두가지 경우뿐이다.
- 노드 사이거리 합을 구하는 각 step에서 결정되지 않은 간선은 $w$를 지키는 선에서 마음대로 정할 수 있으니, 아무 간선도 주어지지 않은 상태에서 최대값은 $n*w$ 이다.
- (2)에 의해 가중치가 주어지면, $(i-1)$→ $i$ 의 값은 고정이 된다.
그러나 $i+s_i−1$ → $i+s_i$ 의 경우 경로에 간선이 여러개 존재 할 수 있으므로, cnt배열을 관리하여 $cnt[i+s_i-1]==0$ 이 되는 경우에 고정이 되는 것으로 한다.
DFS구현 방식과 최댓값 계산식은 코드를 보며 이야기 해보자
int cur = 0;
vector<vector<int>> f(n); //f[i] : i→pi 간선을 사용하는 2가지 출발 노드 저장
vector<int> cnt(n); //cnt[i] : i→i+1 가는 길에 존재하는 간선 개수
void dfs(int v) {
cur++;
for(auto nxt : adj[v]) { //nxt는 v의 자식노드
f[nxt].push_back(cur-1);
cnt[cur-1]++;
dfs(nxt);
f[nxt].push_back(cur-1);
cnt[cur-1]++;
}
}
트리를 순회하면서, $i$→ $p_i$가중치가 영향을 미치는 출발지가 어디인지 알아내야 하고, 각 노드사이에 몇개의 간선이 있는지 알아내야 한다.
- 리프가 아니라면 f[i]에 i-1을 넣고 i의 자식을 dfs에 넣고 호출한다.
- 리프에 도달하면 $i+s_i-1$ 과 $i+s_i$ 의 LCA까지 cnt[i+s_i-1]을 증가시킨다.
ll sum = 0;
int tot = n;
for(int i=1;i<n;i++) {
ll x,y; cin>>x>>y; x--;
for(auto k : f[x]) {
cnt[k]--;
if(cnt[k]==0) tot--;
}
sum +=y;
cout<<tot*w + sum *(2-tot)<<' ';
}
- y의 길이는 2가지 경로에서만 사용되고, 나머지 미확정 경로에서는 y만큼 전부 감소해야 한다.
Codeforces Round 970 (Div. 3)
D. Sakusrako’s Hobby

→ reachable 한 숫자들은 사이클을 이룬다 : 각 숫자가 한 번씩만 등장하기 때문에 사이클 외에 모양은 존재하지 않는다.
→ 사이클은 같은 score을 가지므로 사이클에 해당하는 숫자를 전부 찾고 나서 값을 넣어준다.
E. Alternating String
- 문자열에서 하나를 지우면 그뒤의 문자들의 인덱스가 1씩 감소한다 → 짝홀이 바뀐다
- $i$ 까지 어떤 문자의 개수를 미리 구해놓아서 시간을 줄인다 → Prefix sum 이용하는 DP
F. Sakurako’s Box
두 개를 선택해 곱한 값의 기댓값을 $P\over Q$ 로 나타낼 때 $P*Q^{-1}(mod\,10^9+7)$ 를 구하시오. 분수에 모듈로 연산이라…
*모듈러 연산 특강
-
모듈러 연산은 더하기, 뺄셈, 곱셉에 대해 성립한다.
-
모듈러 곱셈의 역원 ($a,b$는 정수)
$a(mod\,\,N)$ 의 모듈러 곱셈의 역원은 $ax≡ 1(mod\,\,N)$ 를 만족하는 $x$ 이다 $ax = kN+1$ 이고 $ax-kN=1$ 으로 나타내며 이는 $aN+bM$ 꼴임을 알 수 있다.
-
베주 항등식 : $ax+by = gcd(a,b)$ 를 만족하는 0이 아닌 정수 $x,y$ 가 항상 존재한다.
- $S={m∣m=ax+by>0,x∈Z,y∈Z}$ 에서 $x=a,\,y=b$ 가 가능하므로 $S$는 공집합이 아니며 자연수의 부분집합이다. 자연수의 정렬성에 의해 S는 최소값 $d$를 가진다.
- $d = ak+bl$ 라고 하자, 어떤 $x = au+bv$ 가 $S$에 속하는데 $d$의 배수가 아니라면 $x = qd+r(0<r<d)$ 인데, $r=x−qd=(au+bv)−q(ak+bl)=au−aqk+bv−bql=a(u−qk)+b(v−ql)∈S$ 즉 $r$은 $d$보다 작아야 하는데 $S$ 에 속하므로 모순, 따라서 모든 $S$의 원소는 $d$ 의배수 이다. $|a|,|b|$ 가 $S$에 속하기 때문에 $d$ 는 $a,b$ 의 공약수이다.
- 어떤 수 $e$ 가 $a,b$ 의 공약수 이면 $d = ak+bl = e(a’k+b’l)$ 이므로 $e$는 $d$의 약수이다. 따라서 $d = gcd(a,b)$ 이다
즉, $x,y$ 가 정수일 때, $ax+by$ 로 가능한 값은 $gcd(a,b)$ 의 배수이다
즉, $x,y$ 가 정수일 때, $ax (mod\,\,b)$ 로 가능한 값은 $gcd(a,b)$ 의 배수이다
$ax-kN=1$ 이 말하는 것은 1이 $gcd(a,N)$ 의 배수이어야 하므로 $gcd(a,N) = 1$ 즉 서로소일 때만 $a$의 $N$에 대한 모듈러 곱셈의 역원이 존재한다.
-
유클리드 호제법 : $a$를 $b$로 나눈 나머지를 $r$이라고 하면 $gcd(a,b)=gcd(b,r)$ 이다
$a = bq+r$ 일때, $g = gcd(a,b)$ 라고 하면 $g|a,g|b$, $r = bq-a$이므로 $g|r$ $g = gcd(b,r)$ 이라고 하면, $g|b,g|r$, $a = bq+r$ 이므로 $g|a$ 따라서 위 방법을 계속해서 진행하면 $(g,0)$의 형태가 나오게 된다. $O(logN)$
int gcd(int a,int b) { return b? gcd(b,a%b) : a; } -
확장 유클리드 호제법 : $ax+by=d=gcd(a,b)$ 를 만족하는 $(x,y)$ 를 구할 수 있다.
- $a=bq_0+r_1$ 을 $ax+by=d$ 에 대입하면 $b(q_0x+y)+r_1(x)=d$ 즉, $(a,b)$ 에 대한 문제를 $(b,r)$ 에 대한 식으로 줄인 것이다.
- 계속해서 범위를 줄이면 $(d,0)$ 까지 줄어들고 이때 $x_i=1,y_i=0$ 이 성립한다.
- 이 값을 가지고 재귀적으로 점점 더 큰 범위로 올라간다면 진짜 $x,y$ 를 알 수 있지 않을까?
$a$의 계수를 $s$ , $b$의 계수를 $t$라 하고 1번 문장과 $ t_0=s_1-q_0s_0$ , $s_0=t_1 $ 을 보면 재귀적으로 $x,y$ 를 구할 수 있게 된다.
ll exEuclid(ll a,ll b,ll& s,ll& t) { //gcd를 리턴하고 s,t를 갱신하는 함수 if(b==0) {s=1; t=0; return a;} ll gcd = exEuclid(b,a%b,s,t); ll tmp = t; t = s-(a/b)*t; s = tmp; if(s<=0) {//역원이 양수가 되도록 s+=b; t-=a; } return gcd; }식으로 한 번 살펴보자
$a = r_1, b= r_2$
$a=bq_0+r_2$ $b= r_2q_1 + r_3$ $…$ $r_{i−1}=r_iq_i+r_{i+1}$
$r_{i+1} = 0$ 일 때 알고리즘이 종료되고 $r_i = d = gcd(a,b)$
$r_i = s_ia+t_ib$ 를 $r_{i+1} = r_{i-1}-r_iq_i$ 에 대입하면 $s_{i+1}a + t_{i+1}b = (s_{i-1}-s_iq_i)a + (t_{i-1}-t_iq_i)b$
-
모듈러 연산에서 곱셈의 역원
$ax\equiv 1(mod\,\,n)$ 인 $x$를 찾아라 → $ax+ny=1$ 만족하는 $x$ 찾아라 → $1=gcd(a,n)$ 일때만 $(x,y)$ 존재 → $a,n$ 서로소 일때만 역원 존재
exEuclid(a,n,s,t); // s가 역원이 된다- 이렇게 구한 곱셈의 $x$ 는 유일한가요?? $x1,x2$ 가 곱셈의 역원이라고 하면, $n|(ax_1-1)$ , $n|(ax_2-1)$ 이므로 $n|(a(x_1-x_2))$ $a,n$ 서로소 이므로, $n|(x_1-x_2)$ 이므로 $x_1\equiv x_2 (mod\,\,n)$
-
문제로 돌아와서 $P$는 숫자 중 2개를 골라서 곱한 값들의 합 $Q$ 는 $_nC_2$ 이므로 presum 값을 잘이용해 구한 후 $P(mod\,10^9+7) * Q^{-1}(mod\,10^9+7)$ Q의 모듈러 곱셈역원을 구하면 된다.
- $mod$ 값이 소수라면 페르마의 소정리를 사용할 수 있다. 이 포스팅을 끝내고 정수론 모음집을 하나 작성해야겠다.
G. Sakurako’s Task
choose $a_i≥a_j$ and assign $a_i = a_i-a_j \;\;or\;\; a_i = a_i+a_j$
$a_1,a_2$ 에 위 작업을 계속해서 작은 수를 만들면 $g=gcd(a_1,a_2)$ 와 $0$ 을 얻게된다. $a$ 의 개수가 늘어나도 이는 동일한데, 이말은 배열의 최소 간격이 $gcd$ 라는 것이다.
for(int i=1;i<n;i++) {
mn = gcd(mn,a[i]);
}
for(int i=0;i<n;i++) a[i] = mn*i;
배열을 처리한 후 이분탐색으로 $mex_k$ 를 찾을 수 있다.
H. Sakurako’s Test
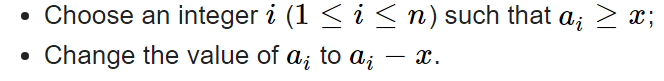
median을 최소화 → 어떤 $x$ 가 주어지면 모든 $a_i = a_i\%x$ 하고 median 구하는게 최적이겠다. $n,q$ 가 모두 10만이라 각 쿼리마다 선형시간 보다 짧은 방법을 찾아서 풀어야 한다.
“$m$ 이 median이 될 수 있다 <=> $a_i\leq m$인 $a_i$가 $n\over2$개 이상이어야 한다”를 떠올리며 문제를 읽어보자 $(1≤a_i≤n)$ 이라는 크리티컬한 조건이 주어져 있는 것을 보고 낌새를 채야한다.
$a_i (mod\,\,x) \leq m$ 개수를 세기 위해서는 가능한 모든 k에 대한 $[kx,kx+m]$ 개수를 세면 된다. $psum$ 을 이용하면 개수세는 것은 $O(1)* {n\over x}$ 의 시간복잡도를 요구한다는 것을 알 수 있다. $x$는 10만 이고 x가 1부터 n까지 $n\over x$ 을 더하는 시간복잡도는 $nlog(n)$ 이라고 한다.
따라서 이분탐색의 시간복잡도 까지 고려하면 $nlog^2(n)$ 의 시간복잡도에 해결 할 수 있다.
- $x$ 로 1이 계속 들어오는 경우가 있기 때문에, 미리 1~n 까지 계산해 놔야 시간초과가 나지 않는다!!
댓글남기기